In structural engineering, section modulus is a geometric parameter of a beam. It is denoted by the letter Z and is a direct measure of the beam’s strength. One of two types of section modulus in engineering is the elastic section modulus Pipes, and other forms of tubing are crucial in the construction of hanging beams. Their distinctive geometry requires a different calculation of the section modulus for this material. It isn’t easy to find the proper formulas for your application on your own. And using incorrect formulas might result in improper bends or unusable goods. Getting your measurements correctly the first time is critical. We are here to provide you all the correct formulas and methods to calculate section modulus pipe correctly.

How section modulus calculations determine steel bending

The flexural strength of a steel section is measured by section modulus. Section modulus is defined as the moment of inertia of the area of a structural member’s cross-section divided by the distance from the neutral axis to the section’s farthest point, as this is where the material changes first. Section modulus is usually expressed in cubic inches / in3 / in3. The section modulus multiplied by the yield strength equals the bending moment required to yield that section.

While evaluating whether a steel section can be curved without heat or not, the section modulus should be calculated. You can find section modulus ratings on a variety of bending equipment. Like  A three-roll sheet metal bender with a section modulus of roughly 1.2 in3, it can bend a 3 x 3 x 3/8 angle and equivalent steel bars, beams, channels, bolts, pipe, and tube. Suppose the section modulus of a particular steel section is determined to generate a value in cubic inches equal to or less than the calculated strength of the bending machine. In that case, the flight forming machine should be able to curve the section.

The Section Modulus’s Foundation

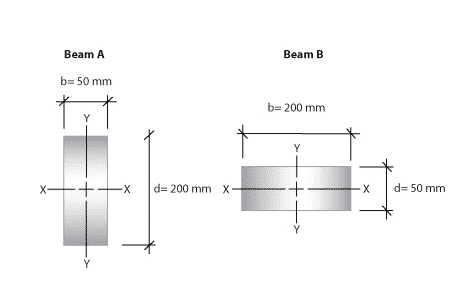
The distribution of relatively more minor fibers or another structural element under consideration can vary significantly between various beams built of different combinations of materials. The ultra-fibers or those at the ends of the sections are pushed to sustain a more significant load. Finding the distance y between the section’s centroid, also known as the neutral axis, is required to calculate the section modulus Z.

Formula to calculate section modulus pipe

Because the shapes of different beams fluctuate with size, the individual formulas for different sections adopt different shapes. A hollow tube, such as a pipe, has a diameter of Z = (4Rπ​)(R4−Ri4​)

Use the following formula/equation to calculate the section modulus:

Z = I divided by y, where I is the moment of inertia and y is the distance between the centroid and the top or bottom edge of the rectangle. D divided by 2 is an equation.

The Z value is the same above and below the centroid for symmetrical sections. Two values are obtained for asymmetrical sections: Z max and Z min.

To find the value of Z for a simple symmetrical shape like a rectangle, use the following formula:

Zxx = I xx divided by y is an equation. Ixx = bd3 divided by 12 equals mm4, and y = 12 depth or d divided by 2 mm.

As a result, the formula for Z is: Z = bd2 divided by six mm3 is an equation.

How to calculate Plastic section modulus

The plastic section modulus, Zx, determines the limit-state of steel beams. It is defined as the point at which the entire cross-section has surrendered.  The plastic section modulus, unlike the elastic section modulus, Sx, has no defined relationship to the cross section’s moment of inertia. However, it is calculated by multiplying the sum of all constituent areas above and below the cross section’s midpoint (x-axis) by the distance between each of the specific elemental centroids and the cross section’s centroid as a whole. Zx = B(H/2)(H/4) + B(H/2)(H/4) = BH2/4. The plastic section modulus for a rectangular cross-section can be calculated by multiplying each section half by the distance between its centroid and the centroid for the entire section: Zx = B(H/2)(H/4) + B(H/2)(H/4) = BH2/4.

Final words

The section modulus is the ratio of the bending moment to the bending stress. Steel with a high section modulus is more difficult to bend and withstand a significant moment without bending stress. To determine if the steel can withstand that much bending moment, divide the maximum bending moment by the section modulus and compare the bending stress to the maximum tensile stress.